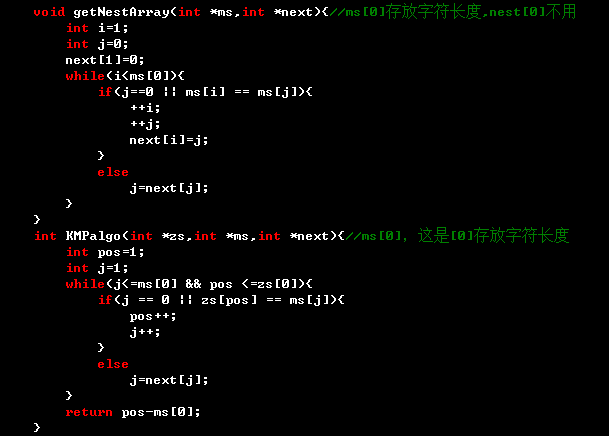
KMP算法细节探索
preface:
想必,很多人都知道D.E.Knuth与V.R.Pratt和J.H.Morris同时提出所谓的狂拽酷炫屌炸天的KMP算法,在对字符串的匹配(或是字符串的查找)方面表现出比较好的效率,该算法对Brute-Force算法的较大改进,具体地讲就是消除了主串指针的回溯,从而使匹配的时间复杂度从O(N2)降低到O(N+M)(N为文本串的长度,M为模式串长度)。其传神之处在于在于针对模式串构造的一个Nest[]数组(该数组只与模式串有关)。
keyword:
KMP算法、增强KMP算法
(扯完了蛋,进入主题。)
Q1:前缀字符串与后缀字符串
A:对于某一字符串来说,约定从第一个字符开始向后的连续若干长度的字符串为前缀字符串,同理从最后一个字符开始向前的连续若干长度的字符串为后缀字符串
case 1:对于字符串“qcer”而言,”qc“为长度为2的前缀字符串,”er“为长度为2的后缀字符串。特殊的,“qcer”既是前缀字符串又是后缀字符串。
Q2:Nest[]数组为何物?
A:Nest[k]定义为在模式串中下标为K位置的前面所有字符串中所有前缀字符串与后缀字符串相等的情况中最长的匹配长度。but,如这等让你我眩晕的表达,不看也罢!一图胜前言!
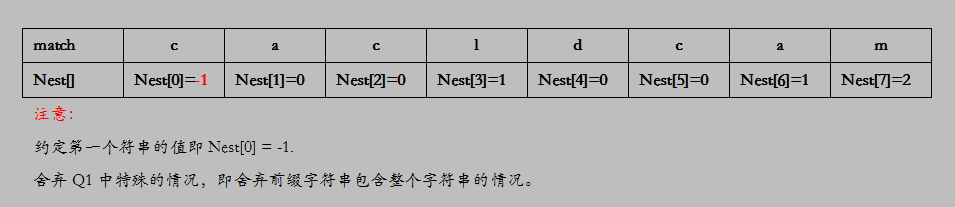
对于Nest[2],下标为2即字符‘c’前面的字符串为“ca”,故没有前缀字符串与后缀字符串想的的情况,其值当然为0。
对于Nest[3],下标32即字符‘l’前面的部分为“cac”,故只有前缀字符串“c”与后缀字符串“c”,其值为1。
其实这个空降的Nest[]数组是很不地道的,既是理解了定义,掌握了其求解方法,还是很没底。而且这TM似乎并没有什么*用,其实不然!
So,下面再给出一种通用的理解方式:
对于求Nest[7]的值,更直观的过程可以如下图:

即把字符串下标为7即字符‘m’之前的字符串“cacldca”从右往左部逐步推进,整个过程在步骤2位置取得正确的值2。步骤3到步骤6中任意一步重叠部分均不能完全匹配(如果有重叠部分完全匹配的情况,那么必然其值比2大)。故不能取到比2更大的值。
首先,理解这个过程度对后面核心算法的匹配过程相当重要。其次,真正求Nest[]数组的值当然不会用这样”too naive“的方法。
如果匹配的过程看做模式串从主串的开始处向右”移动“+匹配的过程,那么KMP不在只是逐步移动,而且还能”跨越式“移动。
Q3:KMP算法为什么能实现”跨越式“移动的原理?
A:先上图!

位置1中,n和m不等,直接跨越过4个字符到位置2处,中间都不用比较就知道不会有匹配成功情况。但是这样做的底气何在??再上图!

因为在位置3到位置6之间绝对不会出现从跌部分想匹配的情况,如果出现那么Nest[7]的值将定会是一个比2大的数,这与Nest[]的定义是相悖的,所以处理3到6的步骤可以自信地省略有木有!!
Q4:Nest[]数组酷炫的解法?
A:想想!还是上图!
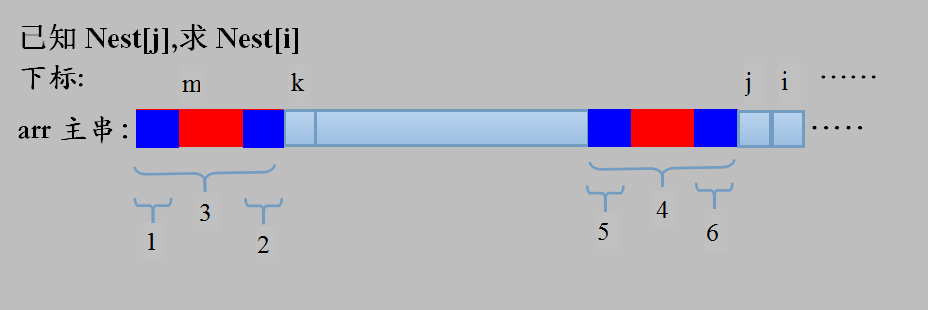
k为位置j的最长前、后缀匹配串3的下一个位置,同理,m为k的最长前、后缀匹配串1的下一个位置。
Nest[j]已知,即对j位置前面的所有串,前缀串3和后缀串4相等且最长;k在j前面,Nest[k]也已知,同理,k前面的所有串,前缀串1和后缀串2相等且最长。
求Nest[i]分两种情况:
1) arr[k] = arr[j];Nest[i] = Nest[j]+1;这是显然的。
2) arr[k] != arr[j];
这时需要我们稍作分析:因为串3=串4,串1=串2,对应必然有,串5=串6,所以必有,串1=串2=串5=串6。
到目前为止由已知只能推出串1=串6,所以,在此基础上尝试扩展串,即判断arr[m]是否等于arr[j]。有趣的此时有分情况两种情况:
1) arr[m = arr[j];Nest[i] = Nest[m]+1;这是显然的。
2) arr[m != arr[j];这又是个很BUG的问题,继续在往前推呗!
也许聪明的你已经明白,没错,递归求解是正解!时间复杂度O(m)(m为模式串长度)。
Code: